O princípio das velocidades virtuais

A Estática é a ciência que estuda o equilíbrio das forças. Entendamos por força como a causa, seja qual for a sua natureza, que imprime ou tende a imprimir movimento a qualquer corpo onde esteja aplicada. Num estado de equilíbrio, a força não produz qualquer tipo de movimento mas pode ser medida por intermédio do efeito que produziria caso não fosse contrariada. As forças aplicadas num corpo podem ser representadas, do ponto de vista geométrico, por vectores, isto é, possuem direcção, intensidade e ponto de aplicação.
Todos os princípios utilizados na resolução de problemas de equilíbrio podem ser resumidos a três essenciais:

• Princípio da Alavanca: princípio idealizado por Arquimedes segundo o qual, uma alavanca carregada com dois pesos está em equilíbrio se forem colocados em ambos os lados de um ponto de apoio e as suas distâncias a esse ponto estiverem em proporção com a respectiva magnitude.
  
  A alavanca da figura encontra-se em equilíbrio se as magnitudes dos pesos são tais que \(P_1d_1=P_2d_2\).
  O apoio da alavanca será carregado com uma força cuja magnitude é igual à soma dos pesos aplicados.
• Princípio da Composição do Movimento: princípio segundo o qual o movimento resultante da aplicação de duas forças a um corpo e em simultâneo é equivalente ao movimento resultante da aplicação das duas forças em separado.
  
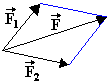
  De acordo com este princípio, duas forças aplicadas num mesmo ponto são equivalentes a uma resultante igual à soma dessas forças de acordo com a regra do paralelogramo, como ilustrado na figura. Esta ideia parece ter surgido pela primeira vez nos trabalhos de Galileu onde este observa que um corpo que se mova com duas velocidades uniformes, uma horizontal e outra vertical, tem uma velocidade única que pode ser representada pela hipotenusa do triângulo rectângulo cujos catetos são as duas velocidades uniformes.
• Princípio das Velocidades Virtuais: designamos por velocidade virtual a velocidade que um corpo em equilíbrio calha em adquirir caso o equilíbrio seja corrompido. Trata-se da velocidade que os corpos adquirirão no primeiro instante do seu movimento sem quebrar as restrições do sistema. O princípio das velocidades virtuais permite afirmar que as forças estão em equilíbrio quando estão em razão inversa das respectivas velocidades virtuais estimadas segundo a direcção destas forças.

Os dois primeiros princípios podem facilmente ser obtidos a partir do princípio das velocidades virtuais. Atentemos na alavanca da figura. Consideramos um deslocamento, sem mover o ponto de apoio, com magnitude \(dx\) na direcção de \(\vec{P}_1\). Uma vez que o ponto de apoio é considerado fixo, apenas se pode dar uma rotação, resultando num deslocamento \(dx'\) na direcção de \(\vec{P}_1\) cuja magnitude depende de \(dx\) e vale

\[dx'=\frac{d_2}{d_1}dx\]

O princípio das velocidades virtuais permite afirmar que

\[P_1dx=P_2dx'=P_2\frac{d_2}{d_1}dx\]

Daqui resulta imediatamente a relação associada ao princípio da alavanca. Se permitirmos um movimento segundo a direcção vertical, tendo em atenção a força aplicada sobre o apoio, imediatamente obtemos o resultado pretendido.
Quanto ao segundo princípio, a ideia subjacente é um pouco mais intrincada. Suponhamos, em primeiro lugar, que duas forças com a mesma magnitude estão aplicadas num ponto segundo a mesma direcção mas em sentidos opostos. Se considerarmos um deslocamento virtual segundo essa direcção, o princípio das velocidades virtuais permite dizer que o sistema se encontra em equilíbrio. Suponhamos agora que estamos na presença de um sistema de três forças \(\vec{F}\), \(\vec{F}_1\) e \(\vec{F}\)_2 como ilustrado na figura seguinte.

Consideremos as forças \(\vec{F}_1\) e \(\vec{F}_2\) perpendiculares entre si. Suponhamos que o sistema está restrito a mover-se segundo uma rotação em torno do ponto \(C\) de forma que exista apenas os deslocamento \(dx\) e \(dx'\) segundo as direcções de \(\vec{F}_1\) e \(\vec{F}_2\). Podemos pensar que a força \(\vec{F}_2\) poderá ser compensada por uma força de ligação qualquer (e o deslocamento considerado não tem componente segundo a direcção dessa força). Se fizermos \(\overline{CP}=r\), obtemos \(\overline{CQ}=r\cos\theta\). Daqui resulta imediatamente que

\[\delta\theta=\frac{dx}{r}=\frac{dx'}{r\cos\theta}\]

Aplicando o princípios das velocidades virtuais para este caso obtemos

\[F_1dx=\left(F\cos\theta\right) dx\]

De acordo com este resultado, o sistema está em equilíbrio se \(F_1=F\cos\theta\). Com um raciocínio semelhante, podemos provar que \(F_2=F\cos\left(\frac{\pi}{2}-\theta\right)=F\sin\theta\). Como já vimos que o sistema se encontra em equilíbrio caso \(F=F'\), uma vez que as forças têm a mesma magnitude e direcção mas sentidos opostos, podemos afirmar que \(\vec{F}'\) é equivalente à aplicação das forças \(\vec{F}_1\) e \(\vec{F}_2\) e que pode ser obtida aquando da aplicação da regra do paralelogramo como pretendíamos. Para mostrar que a regra do paralelogramo é válida para um sistema de duas forças não perpendiculares, é suficiente ter em mente que cada uma dessas forças pode ser decomposta num sistema de duas forças perpendiculares, de acordo com o resultado anterior.
Muitos outros princípios que são utilizados em estática podem ser deduzidos com base no princípio das velocidades virtuais, o que demonstra a sua veracidade e generalidade.

Mais detalhes no monumental Mechanique Analytique de Lagrange.