A esfera armilar

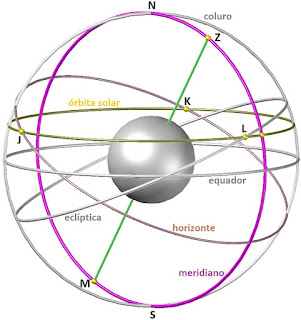
É possível determinar as coordenadas da posição do Sol através da medição da altura da sombra quando este passa pelo meridiano no seu movimento diário aparente. A medição dos valores das sombras ao longo do ano permite determinar, em boa aproximação, qual é a velocidade angular média do Sol na eclíptica. O conhecimento desta velocidade possibilita a estimativa da posição solar em momentos em que o Sol não se encontre a atravessar o meridiano.

A determinação das coordenadas dos outros astros nos sistemas celestes de coordenadas requer o conhecimento da sua posição relativa ao Sol. Tal é possível, medindo as posições daqueles astros que são visíveis durante o dia e durante a noite. A Lua é aquele astro que satisfaz os requisitos com a maior frequência.

As medições podem ser efectuadas com o auxílio de uma esfera armilar. Este instrumento constrói-se do seguinte modo. Consideram-se dois aros, \(1\) e \(2\), com um certo diâmetro, largura e espessura, colocados perpendicularmente sobre a largura de modo que as superfícies curvas estejam contidas numa esfera. O aro \(1\) representa a eclíptica e o outro representa o coluro que contém os pólos da eclíptica e do equador. Estes pólos são marcados sobre o aro \(2\). Apõem-se os aros \(3\) e \(4\), um no interior da superfície côncava dos aros e o outro no exterior das suas superfícies convexas. Os aros \(3\) e \(4\) são permitidos rodar em torno do eixo que contém os pólos do aro \(1\).

No interior do aro interno \(4\) é colocado o aro \(5\) que é permitido rodar no mesmo plano. Dois olhais ou oculares são apostos em pontos diametralmente opostos do aro \(5\). A estes olhais são justapostos dois apontadores para o aro \(4\).

Os aros \(1\) e \(4\) são divididos numa escala angular em graus. No exterior, é colocado um aro \(6\) para suportar a estrutura.

Antes de se proceder à determinação das posições dos astros é necessário alinhar o instrumento com a esfera celeste. Para o efeito coloca-se o instrumento de modo a que as marcações norte-sul se encontrem alinhadas com a direcção do meridiano. Roda-se o dispositivo, em torno do eixo este-oeste em um ângulo igual à latitude do lugar. Este procedimento permite alinhar as marcações com os polos norte e sul celestes. O alinhamento do instrumento fica definido a menos de uma rotação em torno desses pólos. Alinha-se o aro \(3\) externo para o grau no aro \(1\) onde se calculou encontrar o Sol na eclíptica. Com uma rotação em torno dos pólos aponta-se o dispositivo na direcção do Sol de modo a que os aros projectem sombras iguais sobre si mesmos. Este último passo permite alinhar o aro \(1\) com o plano da eclíptica, ficando definida a longitude do ponto dado pela intersecção dos aros \(1\) e \(3\) apontados para o Sol.

Para obter as coordenadas das estrelas, após alinhar a esfera armilar com o Sol muito perto do ocaso, roda-se o aro interno \(4\) de modo a que este bissecte a Lua quando esta é observada do seu plano. O grau assim obtido na eclíptica corresponde à longitude da Lua. A sua latitude obtém-se, rodando o aro \(5\) de modo a que o seu centro seja visível entre as oculares colocadas em posições diametralmente opostas. Estas medições são possíveis apenas quando a Lua se encontra completamente visível durante o dia.

Meia hora mais tarde, quando o astro e a Lua são visíveis, leva-se o aro externo \(3\) para o grau previamente determinado para a lua e roda-se o aparato, em torno dos pólos celestes, de modo a que o plano do aro bissecte a Lua. Rodam-se os aros \(4\) e \(5\) de modo a que a linha de visão do astro passe pelas duas oculares colocadas em posições diametralmente opostas no aro \(5\). Os apontadores apostos às oculares permitem efectuar a leitura da latitude no aro \(4\) cuja posição relativa ao aro \(1\) proporciona a longitude do astro. É importante notar aqui que é necessária uma correcção devida ao movimento da Lua ter uma velocidade angular em longitude aproximada de \(1^{\circ}\) por hora.

Duração dos dias e das noites

O dia solar é definido como o tempo decorrido entre duas transições consecutivas do Sol sobre o mesmo lado do meridiano do lugar relativamente ao horizonte. Define-se o início do dia quando o Sol passa sobre o meridiano perto do nadir. O meio-dia é atingido, portanto, quando a passagem pelo meridiano se verifica perto do zénite.

O dia natural corresponde ao período em que o Sol se encontra acima do horizonte. Durante a noite, por seu turno, o Sol encontra-se abaixo do horizonte e não pode ser observado a partir do lugar. Já foi atrás referido que, na esfera recta, a duração dos dias iguala a duração das noites. No caso da esfera oblíqua, tal acontece apenas quando o Sol se encontra em um dos equinócios. Pretende-se, portando, dada a declinação \(\delta\) do Sol, de onde se pode obter a sua posição na eclíptica, determinar a duração do dia e da noite.

Para o efeito, considere-se um referencial no centro da esfera celeste cujo eixo das abcissas toma a direcção da intersecção  do equador com o meridiano. A direcção das ordenadas é definida pelos pontos \(A\) e \(B\) da intersecção do horizonte com o equador. O eixo das cotas tem a direcção dos polos celestes.

O círculo \(FCD\) representa a órbita solar aparente onde a declinação  é dada pelo ângulo \(EOF\). Note-se que este ângulo não varia quando se considera uma rotação do referencial em torno do eixo das cotas. A equação do plano da órbita é dada por

\[z=\sin\delta\]

considerando que a esfera celeste tem raio unitário. A equação do plano do horizonte é da forma

\[x\cos\varphi+z\sin\varphi=0\]

onde \(\varphi\) é a latitude do lugar. A intersecção do plano do horizonte com o plano da órbita aparente resulta na recta

\[\left\lbrace\begin{array}{l}x=-\tan\varphi\sin\delta\\z=\sin\delta\end{array}\right.\]

A intersecção da recta com a esfera celeste \(x^2+y^2+z^2=1\), considerada como tendo raio unitário, proporciona, em geral, dois pontos \(C\) e \(D\) com coordenadas

\[\left\lbrace\begin{array}{l}x=-\tan\varphi\sin\delta\\ y=\pm\cos\delta\sqrt{1-\tan^2\varphi\tan^2\delta}\\ z=\sin\delta\end{array}\right.\]

Resta determinar o valor do arco \(FC\). Ora, o ponto \(F\) tem coordenadas \(\left(\cos\delta,0,\sin\delta\right)\) e o centro da órbita aparente é o ponto de coordenadas \(\left(0,0,\sin\delta\right)\). Pretende-se, portanto, determinar o ângulo compreendido entre os vectores

\[\left(-\tan\varphi\sin\delta,\cos\delta\sqrt{1-\tan^2\varphi\tan^2\delta},0\right)\]

e

\[\left(\cos\delta,0,\sin\delta\right)\]

Denotando esse ângulo por \(\psi\), a fórmula do produto escalar permite obter

\[\cos\psi=-\tan\varphi\tan\delta\]

O ângulo total que o Sol se encontra acima do horizonte calcula-se como

\[\left\lbrace\begin{array}{ll}2\arccos\left(-\tan\varphi\tan\delta\right), & \left\vert \frac{\pi}{2}-\vert\delta\vert\right\vert\le\left\vert\varphi\right\vert\le\left\vert \frac{\pi}{2}+\vert\delta\vert\right\vert\\ 0, & \left\vert\varphi\right\vert>\frac{\pi}{2}+\delta\\ 2\pi, & \left\vert\varphi\right\vert>\frac{\pi}{2}-\delta\end{array}\right.\]

É claro da fórmula que o ângulo correspondente ao arco da órbita solar visível é sempre igual a \(\pi\) no equador independentemente do valor da declinação \(\delta\). Por outro lado, como \(\vert\delta\vert\le\varepsilon\), torna-se evidente que o arco da órbita solar corresponde à volta completa ou é nulo se o lugar em questão se encontrar no interior dos círculos polares. Sendo a velocidade de transição igual a \(\pi/12\) radianos por hora, a duração do dia vale

\[t=\frac{12}{\pi}\psi\]

dado em horas equinociais.

A esfera celeste

Introdução

A esfera celeste tem sido um elemento fulcral em astronomia. Desde muito cedo se observou que os astros são animados de um movimento diário aparente circular e uniforme no sentido de este para oeste. Por seu turno, alguns dos astros, tal como o Sol, a Lua ou os restantes planetas parecem estar animados de um movimento anual relativamente às estrelas mais longínquas. Esse movimento aparenta dar-se sobre uma esfera que se centra no observador.

A consideração da rotação da Terra de oeste para este permite explicar o movimento médio de rotação de todos os restantes astros no sentido de este para oeste. Muitos filósofos da Grécia Antiga partilhavam esta opinião. Concebido o conceito de rotação diária, resta a questão da sua posição. O facto de que os outros planetas ora se encontram mais próximos, ora mais afastados, sustenta a conclusão de que a Terra poderá não ocupar a posição central da esfera celeste. É concebível, deste modo, que se possa encontrar animada de um movimento de translação. Tal hipótese teria já sido sustentada na Antiguidade Grega, tendo ganho mais notoriedade durante o Renascimento.

Os movimentos dos corpos celestes parecem centrar-se em vários pontos distintos, o que permite concluir que o centro de gravidade da Terra pode não coincidir com o centro dos movimentos universais. A gravidade poderá ser uma propriedade que não lhe seja exclusiva, mas que se estende ao Sol, à Lua ou aos restantes planetas. A ordenação em altura dos planetas, considerando que os planetas interiores, cujas elongações (desvios angulares aparentes máximos) do Sol são limitadas, se encontram abaixo do Sol e os planetas exteriores acima, não é suficiente para explicar o facto de que a Lua, que constitui o astro mais baixo, apresenta todos os valores da elongação. A ordenação obtida do princípio de que os astros mais elevados possuem períodos maiores parece ser violada quando se considera o modelo geocêntrico, mas mantém-se se se considerar o modelo heliocêntrico. A consideração de que os planetas interiores orbitam o Sol teria já sido considerada por escritores do Império Romano.

A ordem dos movimentos parece melhor ser explicada pela consideração de que a Lua orbita a Terra num movimento circular e que o conjunto dos dois astros se encontram animados de um movimento de translação em torno do Sol, encontrando-se aí o centro dos movimentos dos restantes planetas.

A Terra, por seu turno, encontra-se animada de um movimento duplo. O movimento de rotação permite explicar o movimento médio diário dos restantes astros. O seu centro encontra-se animado de um movimento de translação ao longo da eclíptica de oeste para este. O eixo de rotação possui uma inclinação relativamente ao eixo do movimento de translação. A inclinação do eixo mantém-se essencialmente constante durante um intervalo de tempo da ordem do ano. O mesmo se passa com a direcção da projecção do eixo de rotação no plano da órbita que também se mantém constante na mesma ordem de intervalos de tempo. Na realidade, o eixo de rotação também se encontra animado de um movimento à semelhança do que acontece com um peão.

Os círculos notáveis

O movimento de rotação da Terra é dado em torno do eixo que define a direcção norte-sul. Os polos norte e sul deste movimento de rotação projectam-se nos polos norte \(N\) e sul \(S\) na esfera celeste. O círculo máximo com centro na origem da esfera perpendicular ao eixo norte-sul é designado por equador.

O movimento de translação da Terra em torno do Sol é sempre realizado sobre o mesmo plano. Assim, o movimento aparente do Sol relativo às estrelas longínquas dá-se sobre o círculo máximo conhecido por eclíptica. Trata-se de um movimento circular não uniforme cujo período remonta a um ano. A eclíptica intersecta o equador no equinócio da primavera \(H\) e no equinócio do outono \(I\). Os pontos \(A\) e \(B\), a norte e a sul do equador, que distam um quadrante dos equinócios ao longo da eclíptica são designados respectivamente por solstício de verão e solstício de inverno. A eclíptica possui uma inclinação \(\varepsilon\) relativamente ao equador, igual aos ângulos \(PON\) ou \(EOA\), com um valor aproximado de \(23^{\circ}\).

A rotação dos pontos \(A\) e \(B\) que correspondem aos solstícios traçam dois círculos menores designados por trópicos. A rotação do ponto \(A\) define o trópico do caranguejo e a rotação do ponto  \(B\), o trópico do capricórnio. A rotação dos polos \(P\) e \(Q\) da eclíptica, isto é, dos pontos da esfera celeste que estão contidos no eixo que lhe é perpendicular, geram respectivamente o círculo polar ártico e o círculo polar antártico.

O círculo máximo que contém os polos norte e sul bem como os polos da eclíptica é designado por coluro. Trata-se de um círculo máximo contido num plano que é simultaneamente perpendicular aos planos do equador e da eclíptica.

Esfera recta e esfera oblíqua

Em qualquer lugar à superfície da Terra a direcção vertical é aquela que é dada por um fio-de-prumo em equilíbrio. A direcção vertical do lugar define o zénite \(Z\) directamente acima do observador e o nadir \(M\) abaixo. O círculo máximo perpendicular ao eixo \(ZM\) recebe a designação de horizonte. Trata-se do círculo que separa a zona visível da esfera celeste da zona invisível quando observada do lugar em questão. Pode-se considerar que o horizonte se encontra centrado no centro da Terra uma vez que o raio terrestre é, de um modo geral, insignificante quando comparado com as distâncias aos astros. Ao círculo máximo que contém os polos norte e sul e o zénite dá-se a designação de meridiano.

O zénite de um observador que se encontre no equador terrestre está contido no equador celeste. O horizonte é perpendicular ao equador e contém os pólos da esfera celeste. Diz-se que um observador nestas condições se encontra na esfera recta.

O Sol, no seu movimento diário aparente, parte do ponto \(L\) onde se encontra na eclíptica e descreve uma órbita circular paralela ao equador. Esta órbita é dividida em duas partes iguais pelo horizonte de qualquer observador que se encontre na esfera recta. Dado que o movimento de rotação é uniforme, a duração dos dias é igual à duração das noites nesses lugares. Nestes casos, quando o Sol se encontra no equinócio, irá atravessar o meridiano no zénite do observador. Numa metade do ano irá cruzar o meridiano a sul e na outra metade cruzará o meridiano a norte.

Diz-se que um observador se encontra na esfera oblíqua se não se encontrar na esfera recta. Neste caso, o horizonte não é mais perpendicular ao equador.

Na esfera oblíqua, a duração dos dias iguala a duração das noites apenas quando o Sol se encontra nos equinócios e a sua órbita diária parente coincide com o equador.

Se o zénite do observador se encontrar na região limitada pelos trópicos, existem duas alturas no ano em que o Sol passa exactamente sobre o zénite quando atravessa o meridiano. Numa parte do ano o Sol atravessa o meridiano a norte e na outra parte do ano atravessa o meridiano a sul. De um modo geral, quando o zénite do observador se encontra na região delimitada pelos trópicos, incluindo o equador, as sombras são projectadas a norte ou a sul conforme a altura do ano. Os habitantes dessas regiões recebem a designação de anfiscianos.

Se o zénite do observador se encontrar nas regiões delimitadas pelos círculos polares, o horizonte encontra-se delimitado pelo equador e a eclíptica. Nesta situação, existem alturas do ano em que o Sol não cruza o horizonte durante o seu movimento diário, sendo sempre dia ou noite. Como as sombras se podem projectar em qualquer direcção, os habitantes desses lugares são denominados por periscianos.

Os habitantes cujo zénite se encontra entre os círculos polares e os trópicos são designados por heteroscianos uma vez que as suas sombras se projectam sempre a norte ou sempre a sul consoante se encontrem no hemisfério norte ou no hemisfério sul.